Chapter 10 벡터적분
예제 1-1

Sage 코딩
예제 1-2

Sage 코딩
예제 1-3

Sage 코딩
예제 2-1

Sage 코딩
예제 2-2

Sage 코딩
예제 2-3

Sage 코딩
예제 2-4

Sage 코딩
예제 2-5

Sage 코딩
예제 3-1

Sage 코딩
예제 4-1

Sage 코딩

Sage 코딩
예제 5-1

Sage 코딩
예제 5-3
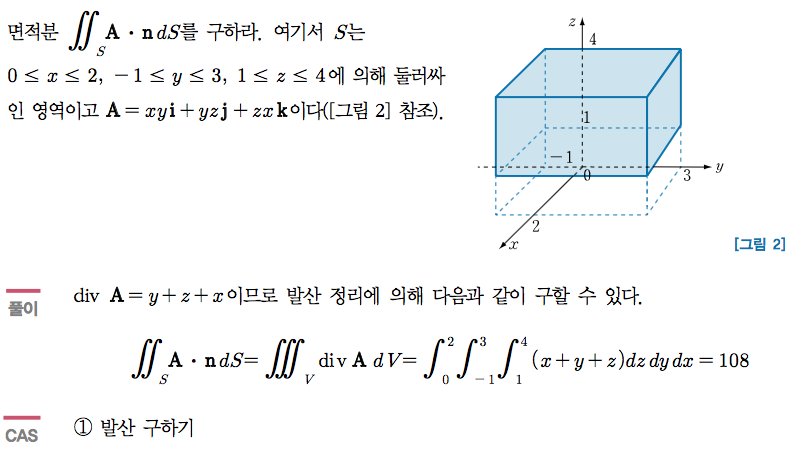
Sage 코딩

Sage 코딩
예제 6-1

Sage 코딩
연습문제

Sage 코딩
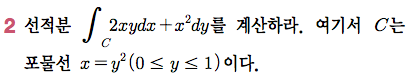
Sage 코딩

Sage 코딩

Sage 코딩

Sage 코딩
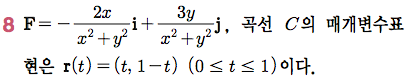
Sage 코딩

Sage 코딩

Sage 코딩

Sage 코딩
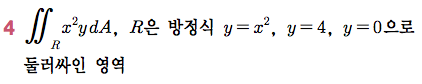
Sage 코딩
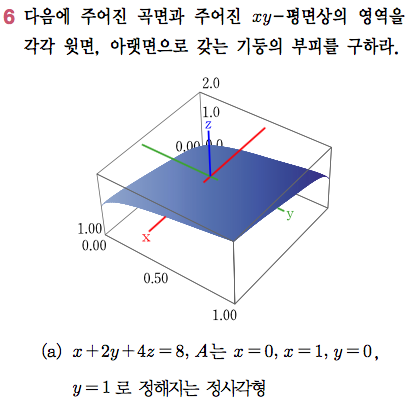
Sage 코딩

Sage 코딩

Sage 코딩
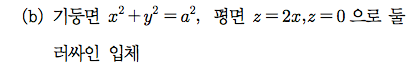
Sage 코딩
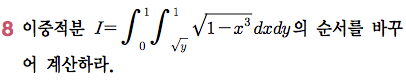
Sage 코딩
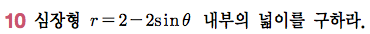
Sage 코딩

Sage 코딩
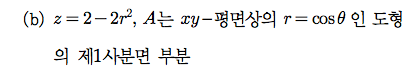
Sage 코딩

Sage 코딩
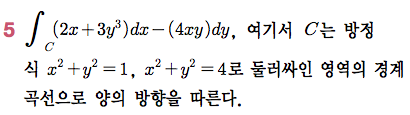
Sage 코딩

Sage 코딩
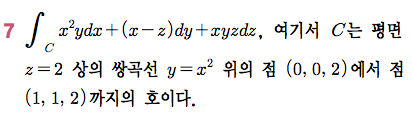
Sage 코딩

Sage 코딩
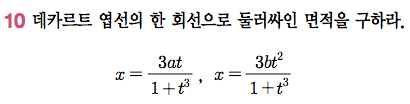
Sage 코딩
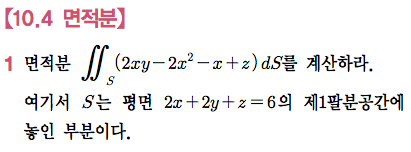
Sage 코딩

Sage 코딩

Sage 코딩

Sage 코딩

Sage 코딩
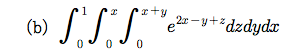
Sage 코딩
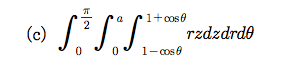
Sage 코딩

Sage 코딩
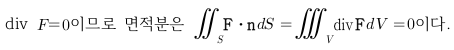

Sage 코딩


Sage 코딩


Sage 코딩
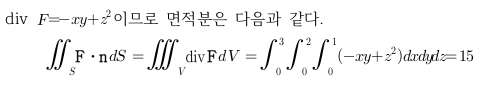
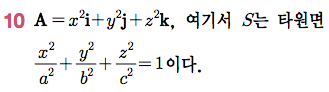
Sage 코딩


Sage 코딩


Sage 코딩
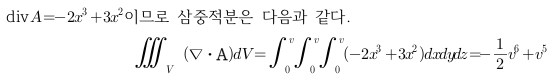

Sage 코딩
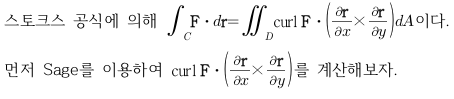
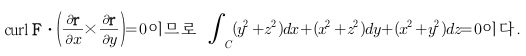
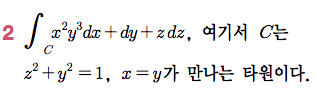
Sage 코딩

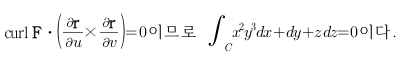

Sage 코딩
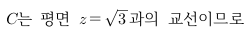
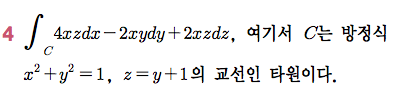
Sage 코딩



Sage 코딩
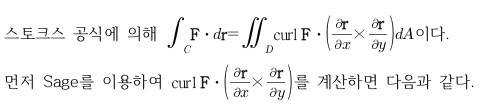
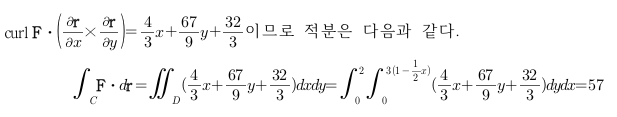

Sage 코딩