Chapter 02 미분방정식의 기초
예제 2-1

Sage 코딩
예제 2-4
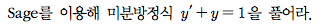
Sage 코딩
예제 2-5

Sage 코딩

Sage 코딩
예제 3-1

Sage 코딩
예제 3-2

Sage 코딩
예제 3-3

Sage 코딩
예제 3-4

Sage 코딩
예제 4-2

Sage 코딩
예제 4-3

Sage 코딩
예제 4-4

Sage 코딩
연습문제
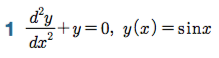
Sage 코딩
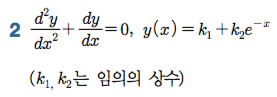
Sage 코딩
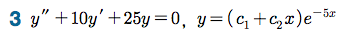
Sage 코딩
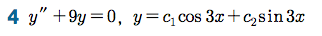
Sage 코딩
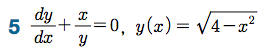
Sage 코딩
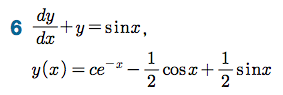
Sage 코딩
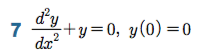
Sage 코딩
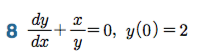
Sage 코딩
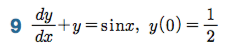
Sage 코딩
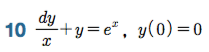
Sage 코딩
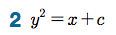
Sage 코딩
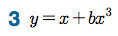
Sage 코딩
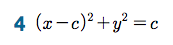
Sage 코딩
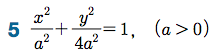
Sage 코딩
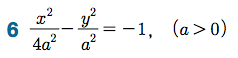
Sage 코딩
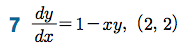
Sage 코딩
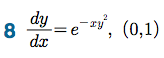
Sage 코딩
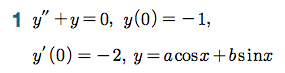
Sage 코딩
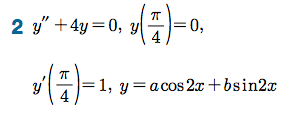
Sage 코딩
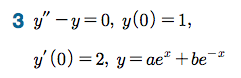
Sage 코딩
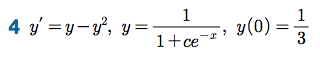
Sage 코딩
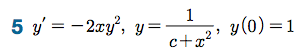
Sage 코딩
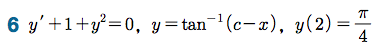
Sage 코딩








